js-data-structures-and-algorithms
Data Structures and Algorithms in JavaScript / TypeScript
By: Nasr Galal / @sniperadmin
This is the most comprehensive explanation for the data structures and algorithms in TypeScript. for the best experience, feel free to visit the full page here:
Material contents
- Material contents
- Run Time Analysis
- Notations for Run Time Analysis
- Guided Examples of Run Time Analysis
- Practical examples for all types
- Digging deeper in calculation of time complexity
- Data Strucutres
Run Time Analysis
An estimate of increasing the runtime of an algo as its input grows
It is used for measuring the efficiency of the algo
Time Factor (Time complexity)
number of operations required for a particular algorithm
Space Factor (Space complexity)
amount of memory required used by an algorithm
Notations for Run Time Analysis
- Omega Notation
– Best Case
- Big O Notation
– Worst Case
- Theta Notation
– Average Case
Omega Notation )
- Gives Lower bound of an algorithm
- Used to measure the best case of the algorithm
Big O notation )
- Gives Upper bound of an algorithm
- Used to measure the worst case of the algorithm
Theta notation )
- Gives average for both Lower & Upper bound of an algorithm
- Used to measure the average case of the algorithm
Guided Examples of Run Time Analysis
| Complexity | Name | Example |
|---|---|---|
| Constant | Adding element in front of a linked list | |
| Logarithmic | Searching an element in a sorted arr / linked list | |
| Linear | Searching element in a unsorted array | |
| Linear algorithmic | Merge sort algorithm | |
| Quadratic | shortest path between 2 points in a graph | |
| Cubic | Matrix Multiplication | |
| Exponential | Naive solution for the nth Fibonacci problem | |
| Factorial | Naive solution for travelling salesman problem |
Practical examples for all types
Constant time )
- It is not affected by the size of an input
function (n: number): number { const a: number = n * n console.log(a) return a }
Linear time
- Performs n of operations as it accepts n input size
let nums: object = {1,2,3,4,5,6} for (let i: number = 0; i < nums.size(); i++) { console.log(nums[i]) }
Logarithmic Time
- Algo than has running time O(log n) si slightly faster than O(n) [Example Binary Search algo]
const binarySearch = function (nums, target) { // -- T(n)
let left = 0; // --- O(1)
let right = len(nums - 1) // --- O(1)
while (left <= right) { // --- O(n/2)
let mid = left + (right - left) / 2; // --- O(1)
if (nums[mid] == target) { // --- O(1)
return mid; // --- O(1)
}
else if (target > nums[mid]) { // --- O(1)
left = mid + 1; // --- O(1)
}
else { // --- O(1)
right = mid - 1; // --- O(1)
}
}
return -1; // --- O(1)
}
To calculate time complexity
1…….
2…….
3…….
4…….
k…….
After k division length =
TC =>
SC =>
Linear Logarithmic Time: )
It divides the problem into sub problems and then merges them in n time (Example => Merge & sort algorithm)
function mergeSort(nums, left, right) { // -- T(n)
if (right > left) { // -- O(1)
let mid = left + (right - left) / 2; // -- O(1)
mergeSort(nums, left, mid) // -- T(n/2)
mergeSort(nums, mid + 1, right) // -- T(n/2)
merge(nums, left, mid, right) // --O(n)
}
}
function merge() {// -- O(n)}
**Solving it: **
—-» eq.1
–> Divide n by 2
—-» eq.2
substitute eq.2 in eq.1
substitute n by n/4 in eq.1
—-» eq.3
Pattern will be:
let
after substituting in the discovered pattern
Pattern will be:
TC => O(n*log(n))
SC => O(n)
Quadratic Time: )
Bubble sort algorithm takes quadratic time complexity (loop nested inside a loop)
for (let i = 0; i < n; i++) { // o(n)
for (let j = 0; j < n; j++) { // o(n)
// statement here --- O(1)
}
} // -- total O(n^2)
Cubic Time: )
Same principle of
for (let i = 0; i < n; i++) { // o(n)
for (let j = 0; j < n; j++) { // o(n)
// statement here --- O(1)
}
for (let k = 0; k < n; k++) { // o(n)
// statement here --- O(1)
}
} // -- total O(n^3)
Exponential Time )
Very slow algo as input grows up. If n = 100,000 .. then T(n) would be 21000000. (Example => brute forcing algorithm [Backtracking]) —
Factorial Time )
Slowest EVER!
Digging deeper in calculation of time complexity
Example #1
for (let i = 0; i < 10; i++) { // -- O(n)
console.log(i) // -- O(1)
}
— Reject any constants —
TC => O(n)
SC => O(1) — This means that we don’t save any data structures in memory
Example #2
for (let i = 0; i < 10; i += 2) { // -- O(n/2)
console.log(i) // -- O(1)
}
TC => O(n)
SC => O(1) — This means that we don’t save any data structures in memory
Example #3
for (let i = 0; i < 10; i++) { // -- O(n)
for (let j = 0; j < 10; j++) { // --O(n)
console.log(i) // -- O(1)
}
}
| i | j | Execution |
|---|---|---|
| 0 | 0 | |
| 1 | 0 | 1 |
| 2 | 0,1 | 2 |
| 3 | 0,1,2 | 3 |
| 4 | 0,1,2,3 | 4 |
| … | … | … |
| n | 1….(n-1) | n |
Pattern will be:
TC =>
SC => O(1) — This means that we don’t save any data structures in memory
Example #4
let p = 0; // -- O(n)
for (let i = 0; p <= n; i += p) { // -- O(root n)
Do something // -- O(1)
}
| i | j |
|---|---|
| 0 | |
| 1 | 0 + 1 |
| 2 | 0 + 1 + 2 |
| 3 | 0 + 1 + 2 + 3 |
| 4 | 0 + 1 + 2 + 3 + 4 |
| … | … |
| k | 1…. + k |
Taking the stop condition if p > n
Then,
Then,
Then,
TC => O(n)
SC => O(1) — This means that we don’t save any data structures in memory
Example #5
for (let i = 0; i < n; i *=2) { // -- O(n)
console.log(i) // -- O(1)
}
| i | j |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| … | … |
| k |
Taking the stop condition if i >= n
Then
Then
Then
TC =>
SC => O(1) — This means that we don’t save any data structures in memory
Example #6
for (let i = 0; i <= 1; i /=2) { // -- O(n)
console.log(i) // -- O(1)
}
| i | j |
|---|---|
| 0 | |
| 1 | n/ |
| 2 | n/ |
| 3 | n/ |
| 4 | n/ |
| … | n/ … |
| k | n/ |
Taking the stop condition if i < 1
Then
Then
Then
Then
TC =>
SC => O(1) — This means that we don’t save any data structures in memory
Example #7
for (let i = 0; i*i < n; i++) { // -- O(n)
console.log(i) // -- O(1)
}
This will stop if –
Then
Then
TC =>
SC => O(1) — This means that we don’t save any data structures in memory
Data Strucutres
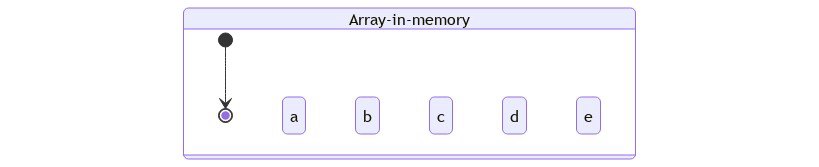
Array
Array is a data structure that contains a group of elements, each is identified by array index.
Properties
- Can store data of different types
- Has contiguous memory location
- Index starts from 0
- Size of array need to be specified and cannot be changed
Example
- Simple Array =>
Types of Array
- One Dimensional Array =>
- Multi-dimenstional Array =>
One Dimensional Array
Each element is represented by a single subscript. Elements are stored in consecutive memory location
Two Dimensional Array
Each element is represented by two subscripts. The Two-dimensional array mxn has m Rows and n columns and contains m*n elements.
for instance 3X4 Array =>
How Array is stored in RAM (Random Accessed Memory)
1D Array
let nums = [1, 2, 3, 4, 5, 6, 7, 8]
let’s assume it will render like this
| . | . | . | . | . | . | . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
The key is that each array value will be converted to a binary equivalent and then will be stored in a memory slot
2D Array
Same concept
How to create 1D Array
- Declare
- Create a reference to the array
- Instantiation
- Create an array
- Initialization
- Assign Values to the array
Declaration of Array
let Example: Array<number> // [1, 2, 3, 4]
let Example: Array<string> // ['a', 'b',...]
Instantiation of Array
let example: Array<number> // [1, 2, 3, 4]
example = new Array()
Initialization of Array
example = new Array()
Searching algorithms
Linear search
Binary Search
The Idea of Binary Search is to divide the array into 2 halfs and must be sorted.
if the target number is larger than the mid value, then we discard the first half and vice versa.
this technique is very powerful.
const nums: Array<number> = new Array(1, 3, 5, 8, 12, 34, 35)
let get = function (arr, index) {
return arr[index];
}
let search = function (arr, target) {
let left: number = 0
let right: number = arr.length - 1;
while (left <= right) {
let mid: number = (left + right) / 2;
if (arr[mid] === target) return mid;
else if (arr[mid] < target) left = mid + 1;
else right = mid - 1;
}
return -1;
}
search(nums, 34)
TC =>
SC => O(1) — This means that we don’t save any data structures in memory
2D Arrays
let x: Array<number> = new Array(2);
for (let i = 0; i < x.length; i++) {
x[i] = new Array(2);
}
x[0][0] = 1
x[0][1] = 2
x[1][0] = 3
x[1][1] = 4
This initialization costs only
Linked List
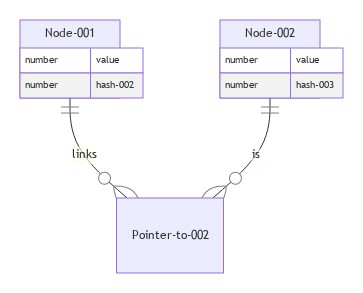
It is a dynamic data structure where each element (node) is made up of two items [data and Reference (pointer) that points to the next node].
| Linked List | Array |
|---|---|
| Size is not fixed | size is always fixed |
| Cannot access a random node | Can access a random node |
| Stored in a non-consecutive memory location | Stored in a contiguous memory location |
Array stored in memory
Because the only ref for each node in the array is the node index itself, the array is stored in memory only in a consecutive memory location.
Linked List visualization
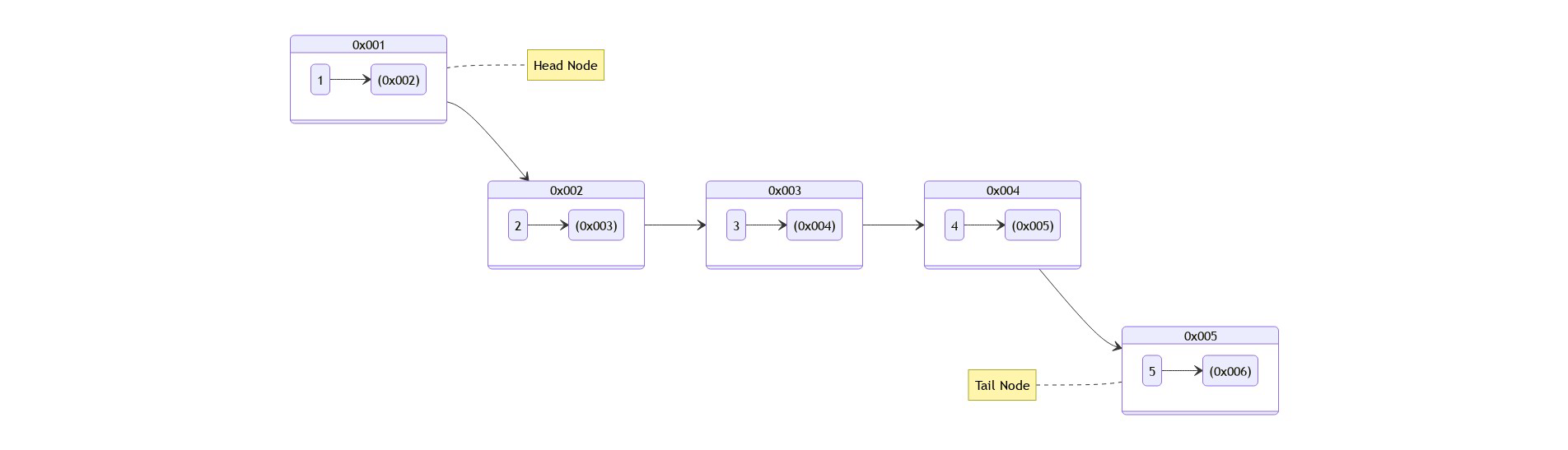
Linked List stored in memory
It could be something like this. Each node is linked to the next one. but they are scattering in different memory slots.
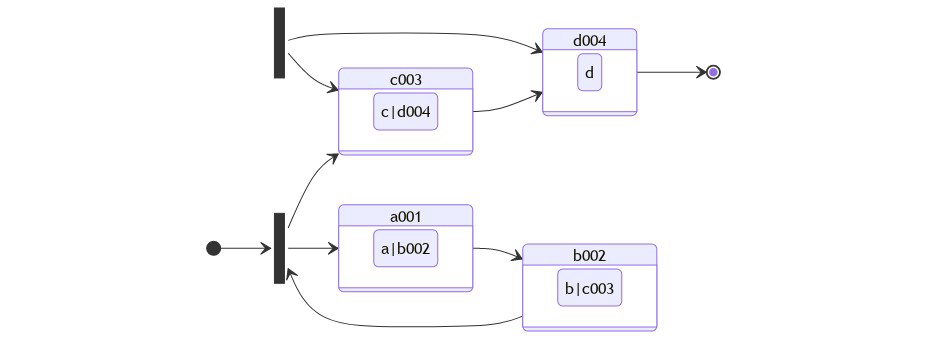
Types of linked lists
- Singly Linked List
- Circular Singly Linked List
- Doubly Linked List
- Circular Doubly Linked List
Singly Linked List
- Each node in the linked list stores the data of node and a reference to the next node.
- Does not store references for previous nodes.
Circular Singly Linked List
- End node is connected to the first node

Doubly Linked List
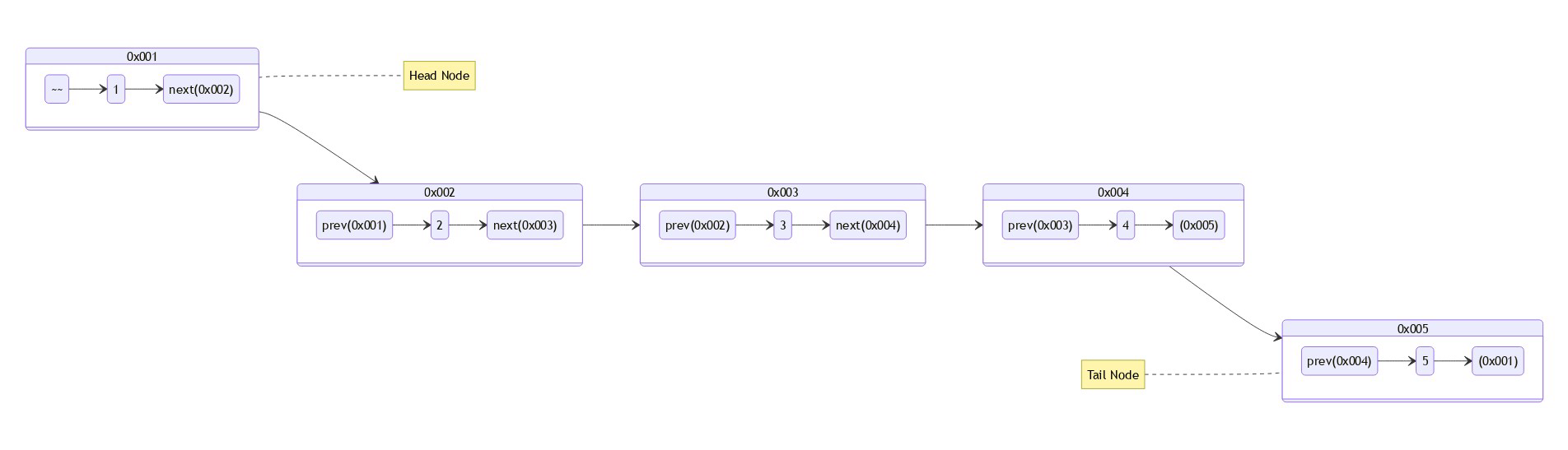
Circular Doubly Linked List
 —
—
Stack
It is a data structure used to store a collection of objects in memory.
LIFO Principle of Stack
LIFO => Last In First Out
- Putting an item on top of the stack is called push
- Removing an item is called pop
LIFO visualization
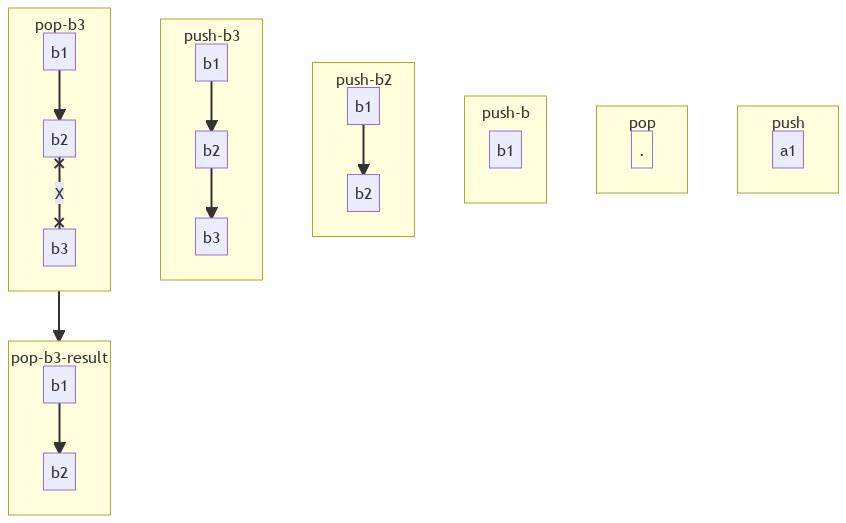
Operations in Stack
- Push: Add element to the top of the stack.
- Pop: Remove element from the top of the stack.
- IsEmpty: Check if stack is empty.
- IsFull: Check if stack is full.
- Peek: Get the value of the top element.
Implementation option of stack
Stack can be implemented in two ways:
- Using Array
- Using linked list
Array implementation
Pros:
- Easy implementation
Cons
- Fixed size
Methods
- push()
- pop()
- peek()
- isEmpty()
- isFull()
- deleteStack()
Linked List implementation
Pros:
- Variable Size
Cons
- Moderate to implement (hard setup)
Methods
- push()
- pop()
- peek()
- isEmpty()
- deleteStack()
